I. Giá trị theo thời gian của 1 khoản tiền
1.1. Giá trị tương lai của tiền
Khái niệm: Giá trị tương lai của một khoản tiền là giá trị của một khoản tiền có thể nhận được tại một thời điểm trong tương lai bao gồm số tiền gốc và số tiền lãi tính đến thời điểm xem xét.
Số tiền lãi sinh ra trong khoảng thời gian từ hiện tại đến tương lai nhiều hay ít phụ thuộc vào lãi suất và cách tính lãi. Vì có 2 cách tính lãi là lãi đơn và lãi kép nên khi tính giá trị tương lai của tiền chúng ta có 2 công thức: Tính giá trị tương lai theo lãi đơn và tính giá trị tương lai theo lãi kép.
Giá trị tương lai của một khoản tiền theo lãi đơn được tính theo công thức:
Fn = P0 (1+ r × n)
Trong đó:
- Fn : Giá trị tương lai tại thời điểm cuối kỳ thứ n
- P0 : Số tiền gốc
- r : Lãi suất của một kỳ tính lãi
- n : Số kỳ tính lãi
Tuy nhiên, việc tính giá trị tương lai theo phương pháp lãi đơn rất đơn giản và ít được áp dụng.
Giá trị tương lai của một khoản tiền theo lãi kép được tính theo công thức:
FVn = P0 (1+ r )n
Trong đó:
- FVn : Giá trị tương lai tại thời điểm cuối kỳ thứ n (Future value);
- P0 : Số tiền gốc;
- r : Lãi suất của một kỳ tính lãi;
- n : Số kỳ tính lãi.
Trong công thức trên, thừa số (1 + r)n được gọi là thừa số thời giá với lãi suất r và số kỳ n cho trước. Để thuận tiện cho việc tính toán, người ta lập bảng tính sẵn các giá trị (1+r)n, gọi là bảng tài chính. Căn cứ vào bảng tài chính này, có thể dễ dàng tìm được giá trị (1 + r)n với các giá trị tương ứng của r và n.
Trên thực tế, hầu hết mọi hoạt động kinh tế đều xác định tiền lãi trên cơ sở phương pháp lãi kép nên giá trị tương lai theo lãi kép được xác định phổ biến hơn. Kể từ đây, khi đề cập đến các phương pháp xác định thời giá của tiền, chúng ta chỉ vận dụng phương pháp lãi kép.
Ví dụ 1:
Có 100 triệu đồng được gửi tiết kiệm với lãi suất 6,5%/năm. Sau 5 năm, sổ tiết kiệm đó có giá trị bao nhiêu tiền?
Sau 5 năm, số tiền trong sổ tiết kiệm là:
FV5 = 100.(1+ 6,5%)5 = 137,01 triệu đồng
1.2. Giá trị hiện tại của tiền
Các nhà đầu tư không chỉ quan tâm đến giá trị tương lai của tiền, mà ngược lại, họ cũng muốn biết để có một số tiền trong tương lai, thì phải bỏ ra bao nhiêu tiền ở thời điểm hiện tại. Đó chính là giá trị hiện tại của một số tiền trong tương lai.
Khái niệm: Giá trị hiện tại của một khoản tiền là giá trị của một khoản tiền phát sinh trong tương lai được quy về thời điểm hiện tại theo một tỷ lệ chiết khấu nhất định.
Như vậy, đây là bài toán ngược của bài toán xác định giá trị tương lai.
Công thức xác định giá trị hiện tại của một khoản tiền:
PV = FVn (1+r)-n
Trong đó:
- PV: Giá trị hiện tại của khoản tiền phát sinh trong tương lai;
- FVn: Giá trị tương lai tại thời điểm cuối kỳ thứ n;
- r : Tỷ lệ chiết khấu hay tỷ lệ hiện tại hóa;
- n : Số kỳ chiết khấu.
(1+r)-n được gọi là hệ số chiết khấu hay hệ số hiện tại hóa. Có thể sử dụng bảng tra tài chính ở phần phụ lục (bảng số 2) để xác định giá trị của biểu thức (1+r)-n với các giá trị tương ứng là r và n.
Tính giá trị hiện tại của một khoản tiền còn được gọi là tính hiện giá hay chiết khấu giá trị một khoản tiền.
Xem xét công thức tính giá trị hiện tại của một khoản tiền nêu trên có thể rút ra nhận xét:
- Thời điểm phát sinh khoản tiền càng xa thời điểm hiện tại thì giá trị hiện tại của khoản tiền càng nhỏ.
- Tỷ lệ chiết khấu hay tỷ lệ hiện tại hóa càng lớn thì giá trị hiện tại của khoản tiền càng nhỏ.
Như trên đã nêu, lãi suất được coi là giá trị của thời gian và rủi ro. Vì thế, để tính đổi giá trị của một khoản tiền trong tương lai về giá trị hiện tại, người ta phải sử dụng lãi suất như một công cụ để chiết khấu giá trị của tiền theo thời gian.
Ví dụ 2:
Để có được 1 khoản tiền là 600 triệu đồng ở thời điểm 10 năm nữa, nhà đầu tư cần phải có bao nhiêu tiền để gửi tiết kiệm trong vòng 10 năm đó, với lãi suất 7%/năm? Số tiền mà nhà đầu tư cần phải đầu tư trong vòng 10 năm với lãi suất 7%/năm là:
PV = 600(1+7%)-10 = 305,01 triệu đồng
II. Giá trị theo thời gian của một dòng tiền
Trong thực tế, hiện tượng thường gặp là có những khoản tiền (các khoản thu nhập hay chi trả) phát sinh liên tục theo những khoảng thời gian bằng nhau tạo thành một dòng tiền (chuỗi tiền). Như vậy, có thể hiểu: Dòng tiền là 1 chuỗi các khoản thu nhập hoặc chi trả xảy ra qua một số thời kỳ nhất định. Khoảng cách giữa 2 khoản tiền phát sinh liên nhau được tính theo năm, quý, tháng… còn gọi là một kỳ hay một thời kỳ.
Tuỳ theo từng tiêu thức phân loại, dòng tiền có thể chia thành nhiều loại khác nhau. Cụ thể như sau:
– Theo thời điểm phát sinh các khoản tiền, người ta chia dòng tiền thành 2 loại: Dòng tiền phát phát sinh đầu kỳ và dòng tiền phát sinh cuối kỳ.
+ Dòng tiền phát sinh cuối kỳ: Thời điểm phát sinh các khoản tiền ở cuối mỗi kỳ. Ví dụ: Tiền thuê nhà trả vào cuối tháng, lãi trái phiếu nhận được vào cuối mỗi năm…
Ta có sơ đồ về dòng tiền phát sinh cuối kỳ như sau:

Trong đó: PV1, PV2,… PVn là các khoản tiền phát sinh ở các thời điểm cuối kỳ thứ nhất, thứ hai, … thứ n.
+ Dòng tiền phát sinh đầu kỳ: Thời điểm phát sinh các khoản tiền ở đầu mỗi kỳ. Ví dụ: Tiền thuê nhà trả vào đầu các tháng, Tiền học phí đóng vào đầu mỗi học kỳ…
Ta có sơ đồ về dòng tiền phát sinh đầu kỳ như sau:
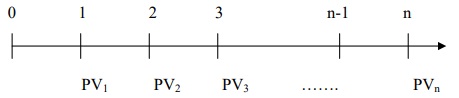
Trong đó: PV1, PV2,… PVn là các khoản tiền phát sinh ở các thời điểm đầu kỳ thứ nhất, thứ hai, … thứ n.
– Theo tính chất của các khoản tiền, dòng tiền được chia thành 2 loại: Dòng tiền đều và dòng tiền không đều.
+ Dòng tiền đều: Các khoản tiền phát sinh ở tất cả các thời kỳ và bằng nhau. Ví dụ: lãi trái phiếu nhận được hàng năm…
Ta có sơ đồ về dòng tiền đều cuối kỳ như sau:
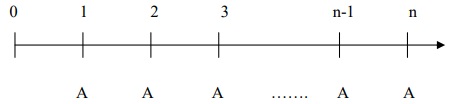
Hoặc sơ đồ dòng tiền đều đầu kỳ như sau:
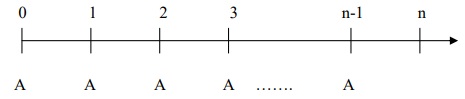
+ Dòng tiền không đều: Các khoản tiền phát sinh ở các thời kỳ không bằng nhau. Ví dụ: Cổ tức nhận được hàng năm…
Ta có sơ đồ về dòng tiền không đều như sau:

Hoặc:
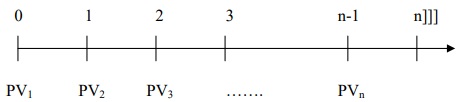
Trong đó: PV1, PV2,… PVn là các khoản tiền phát sinh ở các thời điểm cuối (hoặc đầu) các kỳ thứ nhất, thứ hai, … thứ n và PV1 # PV2 # … # PVn
2.1. Giá trị theo thời gian của dòng tiền phát sinh cuối kỳ
a. Giá trị tương lai của dòng tiền phát sinh cuối kỳ
Tính giá trị tương lai của một dòng tiền phát sinh cuối kỳ thực chất là tính giá trị tương lai của tất cả các khoản tiền phát sinh vào cuối mỗi kỳ rồi cộng lại với nhau.
– Trường hợp đối với dòng tiền không đều:

Ví dụ:
Tại thời điểm 1/1/N, Ngân hàng cam kết cho khách hàng vay 500 triệu đồng trong vòng 5 năm, lãi suất 8%/năm, cam kết giải ngân vào 31/12 hàng năm theo tiến độ 150/100/80/100/70. Tính giá trị tương lai của dòng tiền tại thời điểm 31/12/N+4?
Ta có sơ đồ mô phỏng dòng tiền như sau:
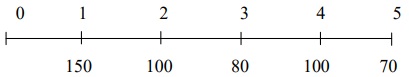
Giá trị tương lai của dòng tiền tại thời điểm 31/12/N+4 là:
150(1+ 8%)4 + 100(1+ 8%)3 + 80(1+ 8%)2 + 100(1+ 8%) + 70 = 601,3565 trđ
– Trường hợp đối với dòng tiền đều:
Đây là trường hợp đặc biệt của dòng tiền không đều. Do PV1 = PV2 =… = PVn = a, vận dụng công thức 1, ta có:

Ví dụ:

b. Giá trị hiện tại của chuỗi tiền tệ phát sinh cuối kỳ
Tính giá trị hiện tại của một dòng tiền phát sinh cuối kỳ thực chất là tính giá trị hiện tại của tất cả các khoản tiền phát sinh vào cuối mỗi kỳ rồi cộng lại với nhau.
– Trường hợp đối với dòng tiền không đều:

Ví dụ:

– Trường hợp đối với dòng tiền đều:

Ví dụ:

2.2. Giá trị theo thời gian của dòng tiền phát sinh đầu kỳ
a. Giá trị tương lai của dòng tiền phát sinh đầu kỳ
– Trường hợp đối với dòng tiền không đều:

– Trường hợp đối với dòng tiền đều:

b. Giá trị hiện tại của dòng tiền phát sinh đầu kỳ
– Trường hợp đối với dòng tiền không đều:

– Trường hợp đối với dòng tiền đều:

(Lytuong.net – Nguồn: topica.edu.vn)

