Công thức tính chỉnh hợp
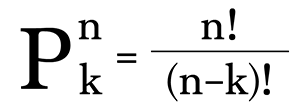
Với n ≥ k ≥ 0.
Chỉnh hợp P (n, r) = n! / (n – r) !. “Số cách lấy tập con có thứ tự gồm k phần tử từ tập n phần tử.” hay chỉnh hợp chập k của n phần tử.
Ví dụ về Bài toán chỉnh hợp
Chọn 3 con ngựa từ nhóm 4 con ngựa
Trong một cuộc đua gồm 15 con ngựa, bạn tin rằng bạn biết 4 con ngựa tốt nhất và 3 trong số đó sẽ về đích ở các vị trí cao nhất: chiến thắng, vị trí và hiển thị (1, 2 và 3). Vì vậy, trong số 4 con ngựa đó, bạn muốn chọn tập hợp con của 3 con ngựa chiến thắng và thứ tự kết thúc của chúng. Có bao nhiêu khả năng cho 3 con ngựa đứng đầu từ 4 con ngựa tốt nhất?
Đối với bài toán này, chúng ta đang tìm kiếm một tập hợp con có thứ tự gồm 3 con ngựa (k) từ tập hợp 4 con ngựa tốt nhất (n). Chúng ta đang bỏ qua 11 con ngựa khác trong cuộc đua 15 con ngựa này vì chúng không áp dụng cho vấn đề của chúng tôi. Chúng ta phải tính P (4,3) để tìm tổng số kết quả có thể xảy ra cho 3 người chiến thắng hàng đầu.
P (4,3) = 4! / (4 – 3)! = 24 khả năng có thể xảy ra
Nếu 4 con ngựa hàng đầu của chúng ta có các số 1, 2, 3 và 4 thì 24 khả năng cho 3 con ngựa giành chiến thắng là {1,2,3}, {1,3,2}, {1,2,4}, {1 ,4,2}, {1,3,4}, {1,4,3}, {2,1,3}, {2,3,1}, {2,1,4}, {2,4 , 1}, {2,3,4}, {2,4,3}, {3,1,2}, {3,2,1}, {3,1,4}, {3,4,1 }, {3,2,4}, {3,4,2}, {4,1,2}, {4,2,1}, {4,1,3}, {4,3,1}, {4,2,3}, {4,3,2}
Xem thêm:

